[LeetCode]2021-04打卡

210401 1006. 笨阶乘

中等 数学

通常，正整数 n 的阶乘是所有小于或等于 n 的正整数的乘积。例如，factorial(10) = 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1。

相反，我们设计了一个笨阶乘 clumsy：在整数的递减序列中，我们以一个固定顺序的操作符序列来依次替换原有的乘法操作符：乘法(*)，除法(/)，加法(+)和减法(-)。

例如，clumsy(10) = 10 * 9 / 8 + 7 - 6 * 5 / 4 + 3 - 2 * 1。然而，这些运算仍然使用通常的算术运算顺序：我们在任何加、减步骤之前执行所有的乘法和除法步骤，并且按从左到右处理乘法和除法步骤。

另外，我们使用的除法是地板除法（floor division），所以 10 * 9 / 8 等于 11。这保证结果是一个整数。

实现上面定义的笨函数：给定一个整数 N，它返回 N 的笨阶乘。

算阶乘

int clumsy(int N) {
    int ans = N * max(1, N - 1) / max(1, N - 2);
    N -= 3;

    while (N > 0) {
        ans += N;
        --N;
        ans -= N * max(1, N - 1) / max(1, N - 2);
        N -= 3;
    }
    return ans;
}

找数学规律

愚人节这道题感觉恶意满满，感觉自己被官方嘲讽了。笨阶乘，笨的人才算阶乘。 \[ \frac{N \times (N - 1)}{N - 2} = \frac{N^2 - N}{N - 2} = \frac{N^2 - 2N + N - 2 + 2}{N - 2} = N + 1 + \frac{2}{N - 2} \] 当 \(N > 4\) 的时候，地板除的 \(\frac{2}{N - 2} = 0\)，所以此时 \(\frac{N \times (N - 1)}{N - 2} = N + 1\)。

int clumsy(int N) {
    if (N <= 4) {
        if (N == 4) 
            return 7;
        else if (N == 3) 
            return 6;
        else 
            return N;
    }

    if ((N & 3) == 0)
        return N + 1;
    else if ((N & 3) == 3)
        return N - 1;
    else
        return N + 2;
}

210402 面试题 17.21. 直方图的水量

困难 动态规划

42. 接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

1
2
3

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例 2：

1 2	输入：height = [4,2,0,3,2,5] 输出：9

提示：

n == height.length
0 <= n <= 3 * 104
0 <= height[i] <= 105

动态规划

int trap(vector<int>& height) {
    int size = height.size();
    vector<int> dpL(size, 0);
    vector<int> dpR(size, 0);

    for (int i = 1; i < size; ++i) {
        dpL[i] = dpL[i - 1] > height[i - 1] ? dpL[i - 1] : height[i - 1];
        dpR[size - i - 1] = dpR[size - i] > height[size - i] ? dpR[size - i] : height[size - i];
    }
    int ans = 0;
    for (int i = 1; i < size - 1; ++i) {
        int minLR = dpL[i] < dpR[i] ? dpL[i] : dpR[i];
        ans += minLR > height[i] ? minLR - height[i] : 0;
    }

    return ans;
}

双指针

左右两个指针

小的先移动大的暂时不动；
上一条移动规则确保了 height[pLeft] < height[pRight] 时，maxL <= maxR。
举例：两个指针总有一遍会是max的状态，当 height[pRight] = maxR > height[pLeft] 时，存在两种情况
1. maxL <= height[pLeft] 此时，maxL < maxR
2. maxL > height[pLeft] 左指针从 maxL 处移动了，所以一定有 maxL < maxR

int trap(vector<int>& height) {

    int pLeft = 0;
    int pRight = height.size() - 1;

    int maxL = 0;
    int maxR = 0;
    int ans = 0;
    while (pLeft < pRight) {
        maxL = maxL > height[pLeft] ? maxL : height[pLeft];
        maxR = maxR > height[pRight] ? maxR : height[pRight];
        if (height[pLeft] < height[pRight]) {
            ans += maxL - height[pLeft];
            ++pLeft;
        }
        else {
            ans += maxR - height[pRight];
            --pRight;
        }
    }
    return ans;
}

210403 1143. 最长公共子序列

中等 动态规划

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

思路：

两个字符串的子序列 => 二维dp数组

int longestCommonSubsequence(string text1, string text2) {
    vector<vector<int>> dp(text1.size() + 1, vector<int> (text2.size() + 1, 0));
    for (int i = 0; i < text1.size(); ++i) {
        for (int j = 0; j < text2.size(); ++j) {
            if(text1[i] == text2[j])
                dp[i + 1][j + 1] = dp[i][j] + 1;
            else
                dp[i + 1][j + 1] = dp[i][j + 1] > dp[i + 1][j] ? dp[i][j + 1] : dp[i + 1][j];
        }
    }
    return dp[text1.size()][text2.size()];
}

210404 781. 森林中的兔子

中等

森林中，每个兔子都有颜色。其中一些兔子（可能是全部）告诉你还有多少其他的兔子和自己有相同的颜色。我们将这些回答放在 answers 数组里。

返回森林中兔子的最少数量。

示例:
输入: answers = [1, 1, 2]
输出: 5
解释:
两只回答了 "1" 的兔子可能有相同的颜色，设为红色。
之后回答了 "2" 的兔子不会是红色，否则他们的回答会相互矛盾。
设回答了 "2" 的兔子为蓝色。
此外，森林中还应有另外 2 只蓝色兔子的回答没有包含在数组中。
因此森林中兔子的最少数量是 5: 3 只回答的和 2 只没有回答的。

输入: answers = [10, 10, 10]
输出: 11

输入: answers = []
输出: 0

说明:

answers 的长度最大为1000。
answers[i] 是在 [0, 999] 范围内的整数。

0331华为笔试第二题

向上取整方法： \[ \lceil \frac{a}{b} \rceil = (a + b - 1) / b \]

int numRabbits(vector<int>& answers) {
    unordered_map<int, int> count_map;
    for (auto i : answers) {
        ++count_map[i];
    }
    int ans = 0;
    for (auto [num, count] : count_map) {
        ans += (count + num) / (num + 1) * (num + 1);
    }
    return ans;
}

210405 88. 合并两个有序数组

简单

给你两个有序整数数组 nums1 和 nums2，请你将 nums2 合并到 nums1 中，使 nums1 成为一个有序数组。

初始化 nums1 和 nums2 的元素数量分别为 m 和 n 。你可以假设 nums1 的空间大小等于 m + n，这样它就有足够的空间保存来自 nums2 的元素。

思路：

从前到后顺序不好控制，但从尾到头稳定 \(O(n)\)

void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
    int i = m-- + n-- - 1;
    while (n >= 0) 
        nums1[i--] = m >= 0 && nums1[m] > nums2[n] ? nums1[m--] : nums2[n--];
}

210406 80. 删除有序数组中的重复项 II

中等

相似：26. 删除有序数组中的重复项

给你一个有序数组 nums ，请你原地删除重复出现的元素，使每个元素 最多出现两次 ，返回删除后数组的新长度。

不要使用额外的数组空间，你必须在 原地修改输入数组 并在使用 \(O(1)\) 额外空间的条件下完成。

双指针

一个指针指示接下来复制到的位置，一个指针指示接下来遍历的元素
- 将接下来遍历的元素跟上两个复制的元素比较，不相等就复制到下一位

int removeDuplicates(vector<int>& nums) {
    int len = 0;
    for (int i : nums) {
        if (len < 2 || i > nums[len - 2])
            nums[len++] = i;
    }
    return len;
}

210407 81. 搜索旋转排序数组 II

中等

已知存在一个按非降序排列的整数数组 nums ，数组中的值不必互不相同。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,4,4,5,6,6,7] 在下标 5 处经旋转后可能变为 [4,5,6,6,7,0,1,2,4,4] 。

给你 旋转后 的数组 nums 和一个整数 target ，请你编写一个函数来判断给定的目标值是否存在于数组中。如果 nums 中存在这个目标值 target ，则返回 true ，否则返回 false 。

提示：

1 <= nums.length <= 5000
-104 <= nums[i] <= 104
题目数据保证 nums 在预先未知的某个下标上进行了旋转
-104 <= target <= 104

进阶：

这是搜索旋转排序数组的延伸题目，本题中的 nums 可能包含重复元素。
这会影响到程序的时间复杂度吗？会有怎样的影响，为什么？

不一样的二分

首先去做了前置题目：33. 搜索旋转排序数组使用了与 153 154 中相同的方法二分查找起始位置，而后根据起始位置取模来进行二分搜索，即可找到元素；

但回到这道题发现了一个问题，当旋转数组中有重复元素的时候，可以查找到数组的起始元素，但没办法找到数组的旋转前的起始位置。

因此需要改变二分的思路，参考了题解后改为了如下过程：

若 nums[mid] == target，直接返回 true；
比较 nums[left] 与 nums[mid] 的关系：
1. nums[left] == nums[mid]
  
  无法判断，只能缩小左侧边界；
2. nums[left] < nums[mid]
  
  左侧区间有序，判断 target 是否在区间中：
  - \(target \in [left, mid)\)
    
    在该有序区间进行二分查找
    
    为了代码简洁，这一步我只更新了区间，效果是一样的。
  - \(target \notin [left, mid)\)
    
    更新区间 \([left, right]\) 为 \([mid+1, right]\)
3. nums[left] > nums[mid]
  
  右侧区间有序，判断 target 是否在区间中：
  - \(target \in (mid, right]\)
    
    在该有序区间进行二分查找
  - \(target \notin (mid, right]\)
    
    更新区间 \([left, right]\) 为 \([left, mid - 1]\)

bool search(vector<int>& nums, int target) {
    int size = nums.size();
    int left = 0;
    int right = size - 1;

    while (left <= right) {
        int mid = (left + right) >> 1;
        if (nums[mid] == target) {
            return true;
        }

        if (nums[left] == nums[mid]) {
            ++left;
        }
        else if (nums[left] < nums[mid]) {
            if (nums[left] <= target && nums[mid] > target) {
                right = mid - 1;
            }
            else {
                left = mid + 1;
            }
        }
        else {
            if (nums[mid] < target && nums[right] >= target) {
                left = mid + 1;
            }
            else {
                right = mid - 1;
            }
        }
    }
    return false;
}

210408 153. 寻找旋转排序数组中的最小值

中等

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次旋转后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：

若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

示例 1：

1
2
3

输入：nums = [3,4,5,1,2]
输出：1
解释：原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。

旋转数组经典题目，跟昨天的题算是兄弟题，二分的方法不同，要注意区分。

二分

思路直接写了 154题可以有重复元素的思路，大体相似。

比较 nums[mid] 和 nums[right] 的大小关系

nums[mid] < nums[right]

说明 \([mid, right]\) 区间内有序，最小元素在 \([left, mid]\) 中，且有可能是 nums[mid]
nums[mid] > nums[right]

说明 \([mid, right]\) 区间内无序，最小元素就在区间内，但绝对不是 nums[mid]
nums[mid] == nums[right]

无法确定最小元素所在的区间，只能左移 right 的位置。
- 为什么左移 right 不会错过最小元素？
  
  即使 nums[right] 为最小，但只要 \(mid \ne right\)，即使跳过 right，也不会错过最小元素。
- 为什么 \(mid \ne right\) ？
  
  只要 \(left \ne right\) ，mid = (left + right) >> 1 可能 \(=left\)，但不可能 \(=right\)。

int findMin(vector<int>& nums) {
    int left = 0;
    int right = nums.size() - 1;

    while (left < right) {
        int mid = (left + right) >> 1;
        if (nums[mid] < nums[right]) {
            right = mid;
        }
        else if (nums[mid] > nums[right]) {
            left = mid + 1;
        }
        else {
            --right;
        }
    }
    return nums[left];
}

一个关注点：为什么都在跟 right 比，但没有跟 left 比，跟 left 比会怎么样？

nums[left] < nums[mid] 时存在两种情况：
1. [1, 2, 3, 4, 5]
  
  这时最小元素在左边
2. [2, 3, 4, 5, 1]
  
  这时最小元素在右边
如果出现上述情况，还需要先比较 nums[left] 和 nums[right] ，若 nums[left] < nums[right]，则直接返回 nums[left]。

210409 154. 寻找旋转排序数组中的最小值 II

困难

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次旋转后，得到输入数组。例如，原数组 nums = [0,1,4,4,5,6,7] 在变化后可能得到：

若旋转 4 次，则可以得到 [4,5,6,7,0,1,4]
若旋转 7 次，则可以得到 [0,1,4,4,5,6,7]

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

给你一个可能存在重复元素值的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

思路 & 代码：同上题。

注意： 旋转数组四道题 33 81、153 154 方法不同，注意区分。

210410 263. 丑数

简单 数学

给你一个整数 n ，请你判断 n 是否为丑数。如果是，返回 true ；否则，返回 false 。

丑数就是只包含质因数 2、3 和/或 5 的正整数。

bool isUgly(int n) {
    if (n <= 0)
        return false;
    while (n % 5 == 0) {
        n /= 5;
    }
    while (n % 3 == 0) {
        n /= 3;
    }
    return !(n & n - 1);
}

位运算细节

为什么不是 n & 1 而是 n & n - 1 ？
- 因为 /3 /5 后，若 n 是丑数将为 2 的幂，也就是二进制表示只会有一位是 1；
- 这时 n & n - 1 将为0；
- 而 n & 1 仅能判断当前 n 是奇数还是偶数。

疑问

为什么负数不算？
- 我是傻子。
- 丑数就是只包含质因数 2、3 和/或 5 的正整数。

预判一下明天的题，先写在这。

210411 264. 丑数 II

中等 数学

编写一个程序，找出第 n 个丑数。

丑数就是质因数只包含 2, 3, 5 的正整数。

示例:

1
2
3

输入: n = 10
输出: 12
解释: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 是前 10 个丑数。

说明:

1 是丑数。
n 不超过1690。

int nthUglyNumber(int n) {
    vector<int> nums;
    nums.push_back(1);
    int p2 = 0, p3 = 0, p5 = 0;

    for (int i = 1; i < n; ++i) {
        int ugly = min(nums[p2] * 2, min(nums[p3] * 3, nums[p5] * 5));
        nums.push_back(ugly);
        if (ugly == nums[p2] * 2) 
            ++p2;
        if (ugly == nums[p3] * 3) 
            ++p3;
        if (ugly == nums[p5] * 5) 
            ++p5;
    }
    return nums[n - 1];
}

210412 179. 最大数

中等

给定一组非负整数 nums，重新排列每个数的顺序（每个数不可拆分）使之组成一个最大的整数。

注意：输出结果可能非常大，所以你需要返回一个字符串而不是整数。

class Solution {
public:
    static bool cmp (const int& a, const int& b) {
        return to_string(a) + to_string(b) > to_string(b) + to_string(a);
    }

    string largestNumber(vector<int>& nums) {
        sort(nums.begin(), nums.end(), cmp);
        string maxNum = "";
        for (int i : nums) {
            maxNum += to_string(i);
        }
        if (maxNum[0] == '0')
            return "0";
        return maxNum;
    }
};

cmp作为成员函数导致的报错

reference to non-static member function must be called

参考

原因：

sort函数本来希望我们传递的cmp函数是一个两个void*参数的函数，咋一看我们也是这么做的，但是由于这是类的成员函数，导致cmp函数在编译时会产生一个implicit parameter，即this指针，所以cmp实际上有三个参数，而sort希望cmp只有两个参数，这就产生了参数不匹配的问题，也就导致了这个错误。

而类的静态成员函数中不会隐式的包含对象的this指针，就不会出现这个问题了。

但为什么错误提示说：必须调用对非静态成员函数的引用，还是不太明白。

谓词

其实就是经过一系列判断并返回True or False的函数。

不明所以主要是翻译的问题，英文名是Predicate，贴一段Effective STL中给出的解释：

"A predicate is a function that returns bool (or something that can be implicitly converted to bool). Predicates are widely used in the STL. The comparison functions for the standard associative containers are predicates, and predicate functions are commonly passed as parameters to algorithms like find_if and the various sorting algorithms."

cmp函数的另一种写法

string largestNumber(vector<int>& nums) {
    sort(nums.begin(), nums.end(), [](const int& a, const int& b) {
        return to_string(a) + to_string(b) > to_string(b) + to_string(a);
    });
    
    string maxNum = "";
    for (int i : nums) {
        maxNum += to_string(i);
    }
    if (maxNum[0] == '0')
        return "0";
    return maxNum;
}

210413 783. 二叉搜索树节点最小距离

简单

给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。

注意：本题与 530：https://leetcode-cn.com/problems/minimum-absolute-difference-in-bst/ 相同

示例 1：

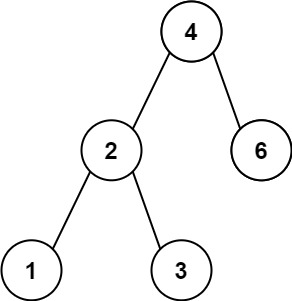
1 2	输入：root = [4,2,6,1,3] 输出：1

示例 2：

1 2	输入：root = [1,0,48,null,null,12,49] 输出：1

提示：

树中节点数目在范围 [2, 100] 内
0 <= Node.val <= 105

一道利用BST特性的简单的中序遍历，递归很简单，再写一遍迭代的中序遍历做练习。

递归

void dfs(TreeNode* root, vector<int>& tree) {
    if (root->left) 
        dfs(root->left, tree);
    tree.push_back(root->val);
    if (root->right)
        dfs(root->right, tree);
}
int minDiffInBST(TreeNode* root) {
    vector<int> tree;
    dfs(root, tree);
    int min = INT_MAX;
    for (int i = 1; i < tree.size(); ++i) {
        min = min > tree[i] - tree[i - 1] ? tree[i] - tree [i - 1] : min;
    }
    return min;
}

迭代

可以通过暂存指针在中序遍历的过程中找到最小差值，可以省去一个数组的空间。

int minDiffInBST(TreeNode* root) {
    vector<int> tree;
    //dfs(root, tree);
    stack<TreeNode*> Nodes;

    while (root || !Nodes.empty()) {
        while (root) {
            Nodes.push(root);
            root = root->left;
        }
        TreeNode* tmp = Nodes.top();
        Nodes.pop();
        tree.push_back(tmp->val);
        root = tmp->right;
    }

    int min = INT_MAX;
    for (int i = 1; i < tree.size(); ++i) {
        min = min > tree[i] - tree[i - 1] ? tree[i] - tree [i - 1] : min;
    }
    return min;
}

Connor

【LeetCode】2021-04打卡

[LeetCode]2021-04打卡

210401 1006. 笨阶乘

算阶乘

找数学规律

210402 面试题 17.21. 直方图的水量

动态规划

双指针

210403 1143. 最长公共子序列

210404 781. 森林中的兔子

210405 88. 合并两个有序数组

210406 80. 删除有序数组中的重复项 II

双指针

210407 81. 搜索旋转排序数组 II

不一样的二分

210408 153. 寻找旋转排序数组中的最小值

二分

210409 154. 寻找旋转排序数组中的最小值 II

210410 263. 丑数

位运算细节

疑问

210411 264. 丑数 II

210412 179. 最大数

cmp作为成员函数导致的报错

谓词

cmp函数的另一种写法

210413 783. 二叉搜索树节点最小距离

递归

迭代